Decentralized Bayesian Learning

Recent technological advances in data acquisition and computation have enabled massive data collection with lower costs, e.g., from Internet-of-Things and smart devices. Consequently, datasets for system modeling and learning are becoming more and more distributed. Data-driven models aggregating information from distributed datasets provide unrivaled capabilities in prediction and decision making over models learned from individual datasets. However, centralized processing of distributed datasets requires transferring all the raw data to a central entity, incurring concerns on communication bandwidth, privacy, and single point of failure.

Without taking into account epistemic uncertainties, models learned by decentralized optimization of a point estimate, such as maximum likelihood and maximum a posteriori, are likely to suffer from poor generalization and overconfident decisions, particularly when the training data is noisy and insufficient for large-scale models. Bayesian learning provides a principled, rigorous framework to process noisy datasets and create uncertainty-aware models for robust decisions and predictions. Bayesian learning employs Bayes’ law to compute or approximate the posterior distribution of unknown model parameters from a prior distribution of the parameters and a data likelihood function. It is a natural approach to quantify uncertainty and learn efficiently without overfitting. Bayesian learning makes explicit use of prior information, which is often used implicitly as regularization in optimization. This project aims to create a theoretical framework for designing and analyzing decentralized Bayesian learning algorithms via gradient-based MCMC and to identify feasible protocols for enhancing communication and computational efficiency of the algorithms and their privacy properties.

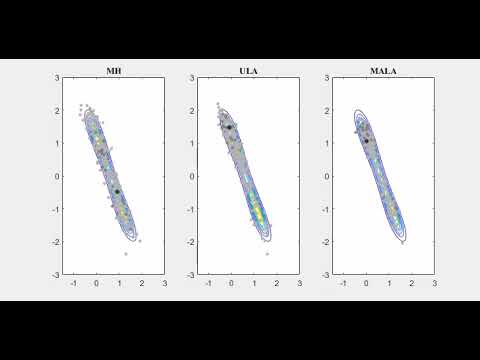
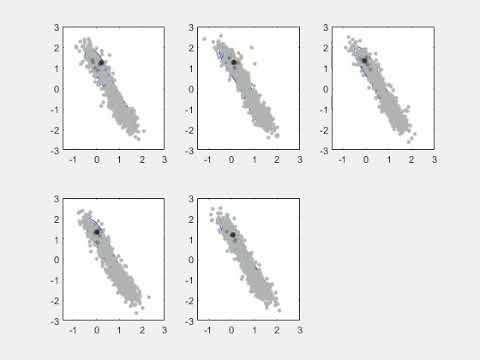
One class of gradient-based MCMC algorithms is derived from the Lagenvin dynamics. The video below (click the picture) shows the comparison between Metropolis–Hastings Sampling (MH), Unadjusted Langevin algorithm (ULA), and Metropolis–Hastings Adjusted Langevin algorithm (MALA) on a bimodal distribution.

sampling algorithms

Our main contributions are investigating decentralized algorithms to achieve MCMC sampling. For example, DULA (decentralized ULA) was developed based on ULA.

DULA

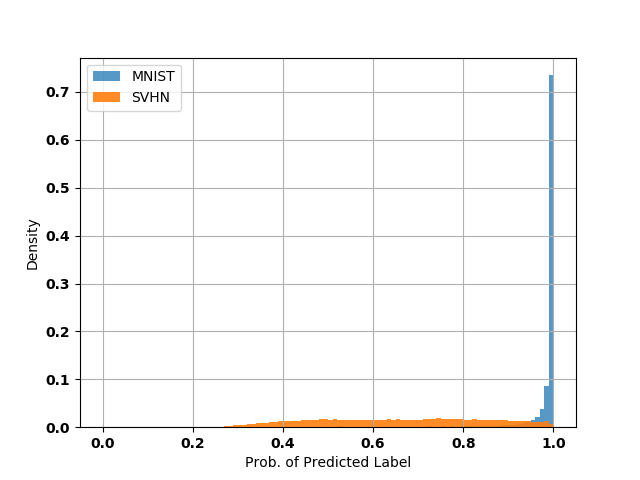
One of the benefits of Bayesian learning is to enable out-of-distribution (OOD) detection. The figure below shows that a Bayesian LeNET learned in a decentralized fashion based on MNIST data responds differently to the SVHN dataset (OOD data).

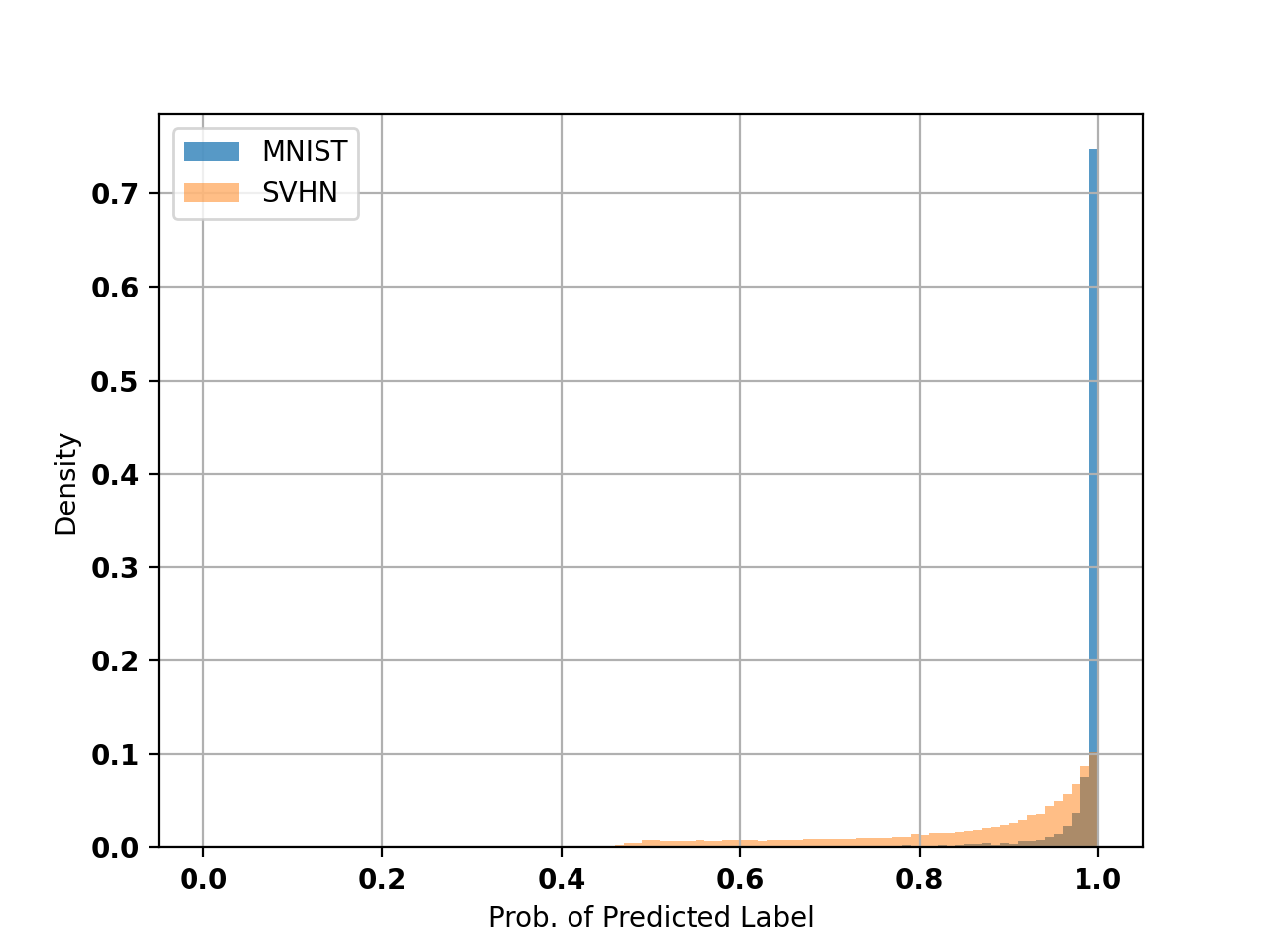
SGD on the other hand responds similarly to the MNIST and SVHN datasets.

Relevant Publications

2024

  1. Approximate constrained stochastic optimal control via parameterized input inference
    Syed, Shahbaz P Qadri, and Bai, He
    Provisionally accepted by Automatica 2024
  2. Decentralized Bayesian Learning via Langevin Dynamics
    Bai, He, Bhar, Kinjal, George, Jemin, and Busart, Carl
    Encyclopedia of Systems and Control Engineering 2024

2023

  1. Asynchronous Local Computations in Distributed Bayesian Learning
    Bhar, Kinjal, Bai, He, George, Jemin, and Busart, Carl
    arXiv preprint arXiv:2311.03496 2023
  2. Distributed event-triggered unadjusted Langevin algorithm for Bayesian learning
    Bhar, Kinjal, Bai, He, George, Jemin, and Busart, Carl
    Automatica 2023

2022

  1. Asynchronous Bayesian Learning over a Network
    Bhar, Kinjal, Bai, He, George, Jemin, and Busart, Carl
    In 2022 IEEE 61st Conference on Decision and Control (CDC) 2022

2021

  1. Distributed Bayesian Parameter Inference for Physics-Informed Neural Networks
    Bai, He, Bhar, Kinjal, George, Jemin, and Busart, Carl
    In 2021 60th IEEE Conference on Decision and Control (CDC) 2021

2020

  1. Decentralized Langevin dynamics for Bayesian learning
    Parayil, Anjaly, Bai, He, George, Jemin, and Gurram, Prudhvi
    Advances in Neural Information Processing Systems 2020